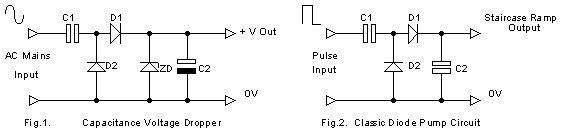
There has been a fair amount written recently about the use of capacitors to "drop" the mains voltage down to values suitable for transistor circuitry. I was recently asked to explain some aspects of such circuitry and looking through my references, was taken by the fact that one of the circuits described looked remarkably familiar.

Above are shown two circuits. Only the bare essentials are shown, things like surge limiting resistors are omitted......... Their similarities are self evident.
Now, if we wish to analyze Fig. 1. in terms of current available, it is natural to think in terms of impedance.
The reactance ( impedance ) of a capacitor is given by the formula ( 1 ) Xc = 1/2
p fC where f is the frequency in Hz and C is the capacitance in Farads. We can now apply Ohms Law to this and we find that, in a circuit where there is capacitance only, ( 2 ) I = 2 p fCE where I is the AC current and E is the RMS value of the AC supply. As D1 is a half wave regulator, ( 3 ) Idc = p fCE.Let us see what a bit of simple arithmetic produces; Iím going to ignore things like voltage drop across diodes :- If we give C1 a value of 470 nf and an AC voltage of 230, equation (2) above gives us :-
2
X p X 50 X 4.7 X 10-7 X 230 = an AC current value of 34 ma. If we use half wave rectification, as in Fig. 1, we should divide this by 2, i.e. 17ma.Taking Fig. 2, we would normally analyze it in terms of charge, it is after all, a charge pump, so we use classic capacitance theory, i.e. Q = CV = IT. ( Charge = Capacitance X Voltage = Current X Time ) or
I = CV/T. As T = 1/f we can write this as Idc = CVf.
If we were to apply the mains to such a circuit we could assume that, because the mains has "unlimited capacity", C1 charges up to twice the mains peak voltage ( i.e. 2(Ö 2 X 230 ) = 650 ), we then get :-
Idc = 2 Ö 2( fCE ) or 2 x Ö 2 x 50 x 4.7 X 10-9 X 2.3 X 102 . This gives us a current of 15 ma.
Now this isnít too much of a discrepancy but it bothers me. The two figures should be the same !
Where is my simple arithmetic going wrong ?
David Ledgard suggested that, if we want to find out why the answers are different, we put the two formulae side by side and cancel out the common factors, So :-
p fCE - - - - 2Ö 2( fCE )
( p x 50 x 470 x 10-9 x 230 ) - - - - ( 2 x Ö 2 x 50 x 470 x 10-9 x 230 )
The result is :- ( p ) - - - - ( 2Ö 2 ) Now, p does not equal 2Ö 2 so this explains why the results are different but does illustrate that we will always get answers in that ratio, no matter what values are used for frequency, capacitance or voltage. The charge formula always gives a current value which is 10% below that calculated using the impedance formula.
Which is correct ? It doesnít really matter ! The tolerances of capacitors are such that there can be a 10% variation anyway !
Nevertheless, I remain puzzled. The two formulae are well established. You might even say that they are pillars of the Electronic Establishment. They should be equally valid and if so the answers should be the sameÖÖ
We have at least a couple of hundred folk in the B.A.E.C. and some of them must be smarter than me.
Come on chaps ! Tell me the answer.