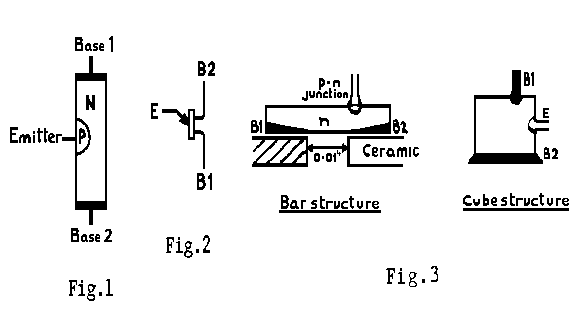
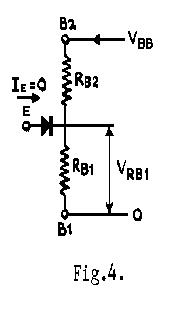
The equivalent circuit shown in Fig.4 has been developed to explain how the device works, and it is necessary to define the terms used in this explanation.


The equivalent circuit shown in Fig.4 has been developed to explain how the device works, and it is necessary to define the terms used in this explanation.
RBB is known as the interbase resistance, and is the sum of RB1 and RB2:
RBB = RB1 + RB2 (1)
N.B. This is only true when the emitter is open circuit.
VRB1 is the voltage developed across RB1; this is given by the voltage divider rule:
RB1
VRB1 = (2)
RB1 + RB2
Since the denominator of equation 2 is equal to equation 1, the former can be rewritten as:
RB1
VRB1 = x VBB (3)
RBB
The ratio RB1 / RBB is referred to as the intrinsic standoff ratio and is denoted by
If an external voltage Ve is connected to the emitter, the equivalent circuit can be redrawn as shown in Fig.5.
If Ve is less than VRB1, the diode is reverse biased and the circuit behaves as though the emitter was open circuit. If however Ve is increased so that it exceeds VRB1 by at least 0.7V, the diode becomes forward biased and emitter current Ie flows into the base 1 region. Because of this, the value of RB1 decreases. It has been suggested that this is due to the presence of additional charge carriers (holes) in the bar. Further increase in Ve causes the emitter current to increase which in turn reduces RB1 and this causes a further increase in current. This runaway effect is termed regeneration. The value of emitter voltage at which this occurs is known as
the peak voltage VP and is given by: VP =
![]() AVVBB + VD (4)
AVVBB + VD (4)
The characteristics of the UJT are illustrated by the graph of emitter voltage against emitter current (Fig.6).
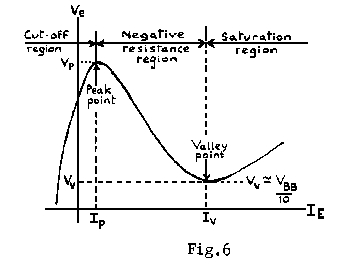
As the emitter voltage is increased, the current is very small - just a few microamps. When the peak point is reached, the current rises rapidly, until at the valley point the device runs into saturation. At this point RB1 is at its lowest value, which is known as the saturation resistance.
The simplest application of a UJT is as a relaxation oscillator, which is defined as one in which a capacitor is charged gradually and then discharged rapidly. The basic circuit is shown in Fig.7; in the practical circuit of Fig.8 R3 limits the emitter current and provides a voltage pulse, while R2 provides a measure of temperature compensation. Fig. 9 shows the waveforms occurring at the emitter and base 1; the first is an approximation to a sawtooth and the second is a pulse of short duration.
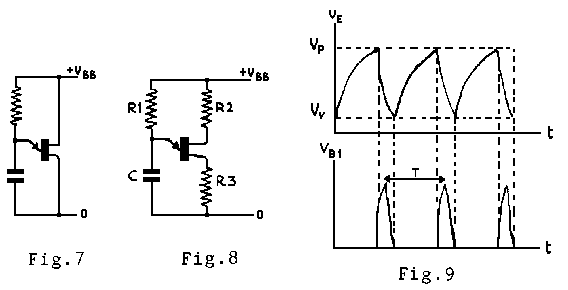
The operation of the circuit is as follows: C1 charges through R1 until the voltage across it reaches the peak point. The emitter current then rises rapidly, discharging C1 through the base 1 region and R3. The sudden rise of current through R3 produces the voltage pulse. When the current falls to IV the UJT switches off and the cycle is repeated.
It can be shown that the time t between successive pulses is given by:
VBB - VV
t + R1C ln secs (5) N.B. R measured in Megaohms. C in µF.
VBB - VP
The oscillator uses a 2N2646 UJT, which is the most readily available device, and is to operate from a 10V D.C. power supply.
From the relevant data sheet the specifications for the 2N2646 are:
VEB2O IE(peak) PTOT(max) IP(max) IV(max)It is important that the value of R1 is small enough to allow the emitter current to reach IP when the capacitor voltage reaches VP and large enough so that the emitter current is less than IV when the capacitor discharges to VV. The limiting values for R1 are given by:Case style TO18 30V 2A 300mw 5µA 4ma 0.56 - 0.75
VBB - VP VBB - VV
R1(max) = and R2(min) =
IP IV
From the specifications for the 2N2646 the average value of So R1(max) = 10 - 7.25/5µA = 550K, and if VV = approx VBB/10, R1(min) = 10 - 1/4mA = 2.25K.If we choose a value for R1 somewhere between these limits, e.g. lOK, the value of C can be calculated from equation (5)
If f = 1MHz, t = 1/f = 1msec. VBB - VP = 10 - 7.25 = 2.75 and VBB - VV = 10 - 1 = 9
t
Rearranging equation(5) to make C the subject: C = VBB - VV
R1 ln
VBB - VP
0.001
so C = = approx 84nF.
104 ln (9/2.75)
Because of component and UJT tolerances it is sufficient in most circumstances to use an approximate formula: f = 1/CR, which assumes that
R2 is not essential; if it is included, a value of 470 ohms is appropriate for the 2N2646. The value of R3 should be small in comparison with RBB, with which it is in series, so as to prevent it from affecting the value of the peak voltage. A value of 47 ohms or thereabouts is satisfactory.
Editor's notes: The above design points are illustrated in the circuit of the enlarger timer which was described earlier this year in the April Newsletter. In that circuit the UJT provides clock pulses at 20Hz. R1 is a combination of a 47K variable and a 150K fixed resistance; R2 is omitted and R3 is 33 ohms. The timing capacitor has a value of 220nF. In addition to the 2N2646, the component list for this timer also includes the TIS43 and the 2N4891. Most suppliers list only the 2N2646, but Maplin also include the TIS43. This device was used with a transistor constant current generator as the sawtooth oscillator in the timebase of the "Student's Oscilloscope" published in "Practical Wireless" in August 1973.
In his book "110 Semiconductor Projects for the Home Constructor" (2nd edition 1978), R.M.Marston gives twenty circuits for UJT projects using the 2N2646. These include pulse and sawtooth generators, analogue/digital converters, relay time delay circuits and frequency dividers. If any member would like to experiment with UJTs there is a good number of 2N2646 and TIS43 in Cyril's stock, and Ray Marston's book can be borrowed from me for 38p postage.
There is also a device called a programmable UJT - the BRY39 is an example so called because its parameters can be set by external components. It is a PNPN device, similar in some ways to a thyristor, and can be used in applications similar to those for the UJT. Perhaps we could have an article about this in a future Newsletter.